连连看游戏消除算法

今天在收到一道的面试题，觉得比较有意思，决定记录下来，整个题目与解答过程大概如下。

连连看是一种很受大家欢迎的小游戏。下面四张图给出了最基本的消除规则：

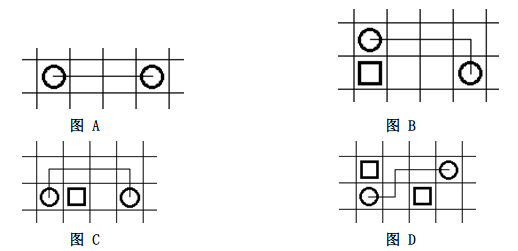
图 A 中出现在同一直线上无障碍的圈圈可以消除；图 B 中两个圈圈可以通过一次转弯消除；图 C 和图 D 中，两个圈圈可以通过两次转弯消除。

已知以下接口，表示位置(x, y)上有无障碍物：

int isBlocked(int x, int y);
return 0;       // 无障碍物（位置(x,y)为空）
return 1;       // 有障碍物（位置(x,y)上有方块或圈圈）

请写一个函数来判断给定的任意两个圈圈是否可消除（x1, y1与x2, y2为两个圈圈的位置）：

int remove(int x1, int y1, int x2, int y2);

水平检测

水平检测用来判断两个点的纵坐标是否相等，同时判断两点间有没有障碍物。

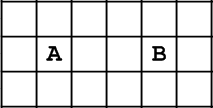
因此直接检测两点间是否有障碍物就可以了，代码如下：

static bool horizon(int x1, int y1, int x2, int y2)
{
    if (x1 == x2 && y1 == y2)
    {
        return false;
    }

    if (x1 != x2)
    {
        return false;
    }

    int start_y = std::min(y1, y2)
    int end_y = std::max(y1, y2);

    for (int j = start_y; j < end_y; j++)
    {
        if (isBlocked(x1, j))
        {
            return false;
        }
    }

    return true;
}

垂直检测

垂直检测用来判断两个点的横坐标是否相等，同时判断两点间有没有障碍物。

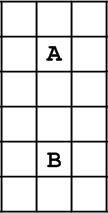
同样地，直接检测两点间是否有障碍物，代码如下：

static int vertical(int x1, int y1, int x2, int y2)
{
    if (x1 == x2 && y1 == y2)
    {
        return false;
    }

    if (y1 != y2)
    {
        return false;
    }

    int start_x = std::min(x1, x2);
    int end_x = std::max(x1, x2);

    for (int i = start_x; i < end_x; i++)
    {
        if (isBlocked(i, y1))
        {
            return false;
        }
    }

    return true;
}

一个拐角检测

一个拐角检测可分解为水平检测和垂直检测，当两个同时满足时，便两点可通过一个拐角相连。即：

一个拐角检测 = 水平检测 && 垂直检测

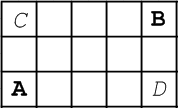
A 点至 B 点能否连接可转化为满足任意一点：

1. A 点至 C 点的垂直检测，以及 C 点至 B 点的水平检测；

2. A 点至 D 点的水平检测，以及 D 点至 B 点的垂直检测。

代码如下：

static int turn_once(int x1, int y1, int x2, int y2)
{
    if (x1 == x2 && y1 == y2)
    {
        return false;
    }

    int c_x = x1, c_y = y2;
    int d_x = x2, d_y = y1;

    int ret = false;
    if (!isBlocked(c_x, c_y))
    {
        ret |= horizon(x1, y1, c_x, c_y) && vertical(c_x, c_y, x2, y2);
    }

    if (!isBlocked(d_x, d_y))
    {
        ret |= horizon(x1, y1, d_x, d_y) && vertical(d_x, d_y, x2, y2);
    }
    if (ret)
    {
        return true;
    }

    return false;
}

两个拐角检测

两个拐角检测可分解为一个拐角检测和水平检测或垂直检测。即：

两个拐角检测 = 一个拐角检测 && (水平检测 || 垂直检测)

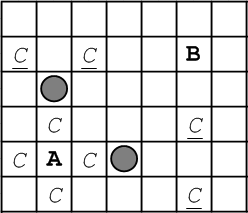
如图，水平、垂直分别穿过 A B 共有四条直线，扫描直线上所有不包含 A B 的点，看是否存在一点 C ，满足以下任意一项：

1. A 点至 C 点通过水平或垂直检测，C 点至 B 点可通过一个拐角连接。（图中用 C 表示）

2. A 点至 C 点可通过一个拐角连接，C 点至 B 点通过水平或垂直连接。（图中用 C 下划线表示）

代码如下：

static int turn_twice(int x1, int y1, int x2, int y2)
{
    if (x1 == x2 && y1 == y2)
    {
        return false;
    }

    for (int i = 0; i <= MAX_X; i++)
    {
        for (int j = 0; j <= MAX_Y; j++)
        {
            if (i != x1 && i != x2 && j != y1 && j != y2)
            {
                continue;
            }

            if ((i == x1 && j == y1) || (i == x2 && j == y2))
            {
                continue;
            }

            if (isBlocked(i, j))
            {
                continue;
            }

            if (turn_once(x1, y1, i, j) && (horizon(i, j, x2, y2) || vertical(i, j, x2, y2)))
            {
                return true;
            }
            if (turn_once(i, j, x2, y2) && (horizon(x1, y1, i, j) || vertical(x1, y1, i, j)))
            {
                return true;
            }

        }
    }

    return false;
}

整合

最后，整合以上四种情况，判断两点是否能消除的代码可以写成：

int remove(int x1, int y1, int x2, int y2)
{
    int ret = false;

    ret = horizon(x1, y1, x2, y2);
    if (ret)
    {
        return 1;
    }
    ret = vertical(x1, y1, x2, y2);
    if (ret)
    {
        return 1;
    }
    ret = turn_once(x1, y1, x2, y2);
    if (ret)
    {
        return 1;
    }
    ret = turn_twice(x1, y1, x2, y2);
    if (ret)
    {
        return 1;
    }

    return 0;
}